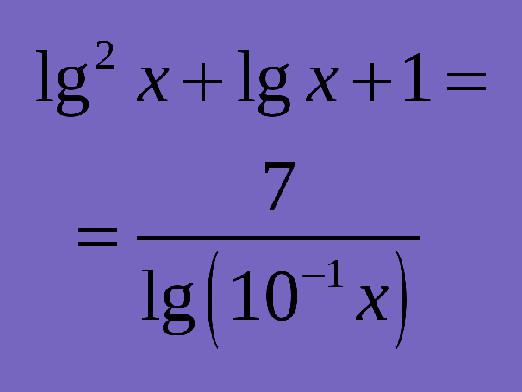불평등을 해결하는 방법?

불평등을 해결하는 방법을 누구나 아는 것은 아닙니다.그들의 구조는 방정식과 유사하고 독특한 특징을 가지고있다. 방정식은 등호가있는 두 부분으로 구성된 연습이며, 불평등 부분 사이에는 "더"또는 "덜"기호가있을 수 있습니다. 따라서 특정 부등식에 대한 해답을 찾기 전에 양 부분을 표현식으로 곱해야 할 필요가있는 경우 숫자의 부호 (양수 또는 음수)를 고려해야한다는 것을 이해해야합니다. 제곱이 곱셈에 의해 수행되기 때문에 불평등 해를 제곱 할 필요가있는 경우 동일한 사실을 고려해야합니다.
불평등을 해결하는 방법
불평등의 시스템을 푸는 것은 훨씬 더 어렵습니다.평범한 불평등. 어떻게 9 클래스의 불평등을 해결하기 위해, 우리는 구체적인 예제로 고려할 것입니다. 제곱 불평등 (시스템) 또는 불평등의 다른 시스템을 해결하기 전에 각 불평등을 개별적으로 풀어서 비교할 필요가 있다는 것을 이해해야합니다. 불평등 시스템의 해답은 긍정적이거나 부정적인 해답입니다 (시스템에는 해가 있거나 해가 없습니다).
과제는 일련의 불평등을 해결하는 것입니다.
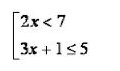
우리는 각 부등식을 개별적으로 풀어 냄

우리는 일련의 해를 나타내는 수선을 구성한다.
답 :

컬렉션은 솔루션 세트의 합집합이므로 번호 줄의이 집합에는 적어도 한 줄의 밑줄이 있어야합니다.
모듈을 사용한 불평등 해법
이 예제는 모듈로 불평등을 푸는 방법을 보여줍니다. 그래서, 우리는 정의가 있습니다 :

우리는 불평등을 해결할 필요가있다.
| x |> 2
이러한 불평등을 해결하기 전에 모듈 (부호)을 제거해야합니다.
정의에 따라 작성해 보겠습니다.

또는

이제는 각 시스템을 개별적으로 해결해야합니다.
우리는 해답 집합을 나타내는 하나의 숫자 선을 만듭니다.
결과적으로, 우리는 많은 솔루션을 결합한 세트를 얻었습니다.
답 :

이차 부등식의 해법
수치 직선을 사용하여 이차 부등식의 해를 고려하십시오. 우리는 불평등이 있습니다.
우리는 이차 삼각 함수의 그래프가 포물선이라는 것을 압니다. 또한 포물선의 가지가> 0 인 경우 위로 향하게됩니다.
x2-3x-4 <0
베트의 정리를 사용하면, 우리는 근원 x1 = -1; x2 = 4
우리는 포물선 또는 오히려 스케치를 그립니다.
따라서 우리는 square trinomial의 값이 -1에서 4까지의 구간에서 0보다 작다는 것을 알게되었습니다.
답 :

이중 문제를 풀 때 많은 의문점이 발생합니다.부등식의 g (X)를 입력 <F (X) <Q (X). 당신이 이중 불평등을 해결하기 전에 간단하고 쉽게로 분해 할 필요가 모든 불평등은 별도로 처리됩니다. 예를 들어,이 예 확장 우리는 부등식의 g (X)의 결과로서 획득 <F (x)와 F (X) <Q (x)는, 해결되어야한다.
사실, 불평등을 해결하기위한 몇 가지 방법이 있으므로 그래픽 방식을 사용하여 복잡한 부등식을 해결할 수 있습니다.
분수 불평등 해법
보다 철저한 접근법에는 분수가 필요합니다.불평등. 이것은 특정 분수 불평등을 해결하는 과정에서 기호가 변할 수 있기 때문입니다. 분수 불평등을 해결하기 전에 간격 방법이 문제를 해결하는 데 사용된다는 것을 알아야합니다. 분수 불평등은 부호의 한쪽이 분수 - 합리적인 표현처럼 보이고 두 번째 - "-0"처럼 표현되어야합니다. 이런 방식으로 부등식을 변환함으로써 결과 f (x) / g (x)>를 얻을 수있다.
간격 법으로 불평등 해소
간격 기술은 완료 방법에 기반합니다.유도, 즉 불평등 해를 찾을 수있는 모든 가능한 변이를 찾는 것입니다. 이 해결 방법은 아마도 8 학년 학생들에게 필요하지 않을 것입니다. 왜냐하면 가장 간단한 운동 인 8 클래스 불평등을 해결하는 방법을 알아야하기 때문입니다. 그러나 오래된 클래스의 경우이 방법은 부분 불평등을 해결하는 데 도움이되므로 바꿔 놓을 수 없습니다. 이 기법의 도움으로 불평등을 해 결하는 것은 0으로 바뀌는 값 사이의 부호를 유지하는 것과 같은 연속 함수의 특성을 기반으로합니다.
우리는 다항식의 그래프를 구성합니다. 이것은 0의 값을 얻는 연속 함수입니다. 즉, f (x)는 점 x에서 0이됩니다.1, x2 및 x3, 다항식의 근원 이 두 지점 사이에 함수의 부호가 유지됩니다.

불평등 f (x)> 0를 풀려면 함수 기호가 필요하므로 그래프를 남겨두고 좌표 선으로 이동하십시오.

f (x)> 0 for x (x1; x2)와 x (x3; )
f (x) x (-; x1)와 x (x2; x3)
그래프는 불평등 해를 명확하게 보여줍니다.f (x) f (x)> 0 (첫 번째 부등식은 파란색, 두 번째 부등식은 빨간색). 결정하기 간격으로 함수의 부호를 결정하려면, 점 중 하나에서 함수의 부호를 알고 있으면 충분합니다. 이 기법을 사용하면 좌변이 인수 분해 된 불평등을 신속하게 해결할 수 있습니다. 불평등에서 뿌리를 찾기가 쉽기 때문에 가능합니다.