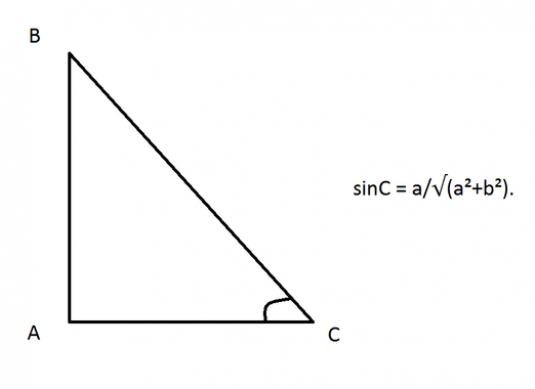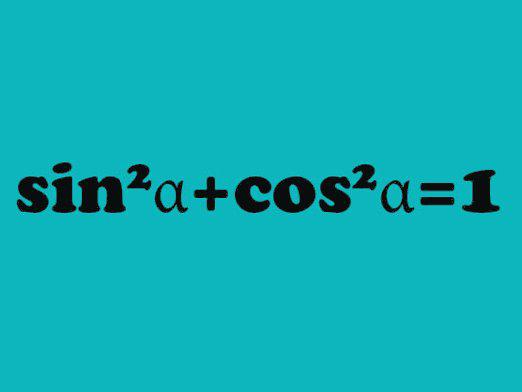각도의 사인을 찾는 방법?

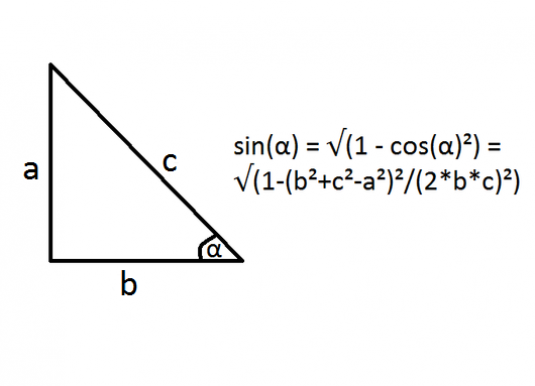
사인 (sin)은 직접 삼각 함수 중 하나입니다. 더 자세한 정보는 사인이란 무엇입니까?라는 기사에서 찾을 수 있습니다.

직각 삼각형의 사인

각도의 사인을 찾는 방법을 알아 내기 전에 규칙을 정의해야합니다. 그것을 직각 삼각형으로 가정 해보자.

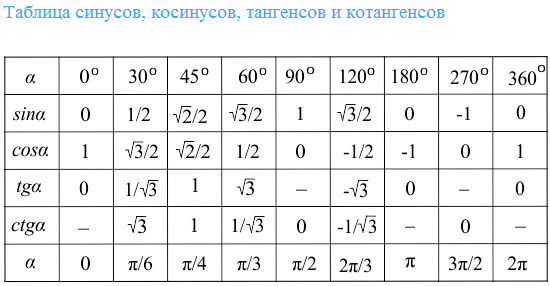
그런 다음 예각의 사인을 찾으려면사각 삼각형의 경우, 빗변 길이에 대한 대칭 다리 길이의 비율을 계산하는 것으로 충분합니다. sin (α) = a / c. 죄 90 °가 항상 1임을 기억하는 것이 가치가 있습니다.

임의의 삼각형에서 각도의 사인 찾기코사인 정리 (cos)를 사용하는 것이 가장 쉽습니다 : 임의의 변의 길이의 제곱은 다른 두 변의 길이의 제곱의 합계와 이중 곱을 뺀 것과 그 사이의 각의 코사인에 동일합니다.

a² = b² + c² - 2 * b * c * cos (α)

cos (α) = (b² + c² - a²) / (2 * b * c)

그리고 같은 각도 sin (α) ² + cos (α) ² = 1이고 이것은 상수이기 때문에 우리는 사인을 결정하기위한 공식을 도출 할 수 있습니다 :

sin (α) = √ (1- cos (α) ²) = √ (1- (b² + c²-a²) ² / (2 * b * c) ²).

더 자세히 설명하면 코사인을 사용하여 각의 사인을 찾는 것은 코사인을 알고있는 경우 사인을 찾는 방법에 대한 우리의 기사에서 고려됩니다.

더 읽기 :