함수 그래프를 어떻게 찾을 수 있습니까?
학생들의 기능을 계획하는 작업대수학 연구의 초창기에 만나서 해마다 계속해서 건설합니다. 선형 함수의 그래프에서 시작하여, 당신은 단지 두 점, 즉 6 점, 과장 및 사인 곡선이 필요한 포물선을 알 필요가 있습니다. 지나가는 해가 갈수록 기능이 점점 더 복잡해지고 그래프의 구성을 템플릿에서 수행 할 수 없기 때문에 미분과 한계를 사용하여보다 복잡한 연구를 수행해야합니다.
함수 그래프를 찾는 방법을 알아 보겠습니다. 이를 위해 가장 단순한 함수부터 시작하여 그래프를 점으로 구성한 다음 더 복잡한 함수를 작성하는 계획을 고려할 것입니다.
선형 함수의 그래프 그리기
가장 간단한 그래프를 만들려면 함수 값 표를 사용하십시오. 선형 함수의 그래프는 직선입니다. 함수 y = 4x + 5 그래프의 점을 찾으려고합니다.
- 이렇게하려면 변수 x의 임의의 두 값을 함수로 대체하고 변수 y의 값을 찾아 모든 것을 테이블에 넣습니다.
- y = 4 * 0 + 5, 즉 y = 5이 값을 0 아래의 테이블에 씁니다. 마찬가지로 x = 0, y = 4 * 1 + 5를 얻습니다. , y = 9.
- 이제, 함수 그래프를 구성하려면 좌표 평면에이 점들을 그려야합니다. 그런 다음 직선을 그려야합니다.
2 차 함수의 그래프 구성
2 차 함수는 y = ax 형태의 함수입니다.2+ bx + c, 여기서 x는 변수이고, a, b, c는 숫자입니다 (a는 0이 아닙니다). 예 : y = x2, y = x2+5, y = (x-3)2, y = 2x2+ 3x + 5.
가장 간단한 2 차 함수 y = x를 생성하려면2 일반적으로 5-7 점을 얻습니다. 변수 x : -2, -1, 0, 1, 2에 대한 값을 취하여 첫 번째 그래프를 작성할 때뿐만 아니라 y의 값을 찾습니다.
2 차 함수의 그래프를 포물선이라고합니다. 기능 그래프를 작성한 후 학생들은 일정과 관련된 새로운 작업을 수행합니다.
예제 1 : 함수 y = x의 그래프 포인트의 가로 좌표 찾기2문제를 해결하려면 함수에 값 9를 대입 할 필요가 있습니다. 우리는 9 = x2 이 방정식을 푸십시오. x = 3 및 x = -3이다. 이것은 함수의 그래프에서 볼 수 있습니다.
함수의 연구와 그래프의 구성
좀 더 복잡한 함수의 그래프를 만들려면 여러 단계를 거쳐야합니다. 이렇게하려면 다음이 필요합니다.
- 함수의 도메인을 찾으십시오. 정의 영역은 변수 x가 취할 수있는 모든 값입니다. 정의의 영역에서, 분모가 0이되거나 방사형이 음수가되는 점을 제외시킬 필요가있다.
- 패리티 또는 홀수 기능을 설정하십시오. 조건 f (-x) = f (x)에 해당하는 함수조차도 짝수임을 상기하십시오. 그 그래프는 Oy를 기준으로 대칭입니다. 이 함수는 조건 f (-x) = - f (x)에 해당하는 경우 홀수가됩니다. 이 경우 그래프는 원점을 기준으로 대칭입니다.
- 좌표축과의 교점을 찾으십시오. 축선 Ox과의 교점의 횡좌표를 찾으려면 방정식 f (x) = 0 (이 경우 세로 좌표는 0 임)을 풀어야합니다. Oy 축과의 교점의 좌표를 찾으려면 함수 x에 0을 대입해야합니다 (가로 좌표는 0 임).
- 함수의 점근선을 찾으십시오. Asipotite는 그래프가 무한히 접근하는 직선이지만 결코 교차하지 않습니다. 함수 그래프의 점근선을 찾는 방법을 알아 봅시다.
- 수직 점근선은 x = a 형식의 직선입니다.
- 수평 점근선은 y = a 형식의 직선입니다.
- 비스듬한 점근선은 y = kx + b 형태의 직선이다.
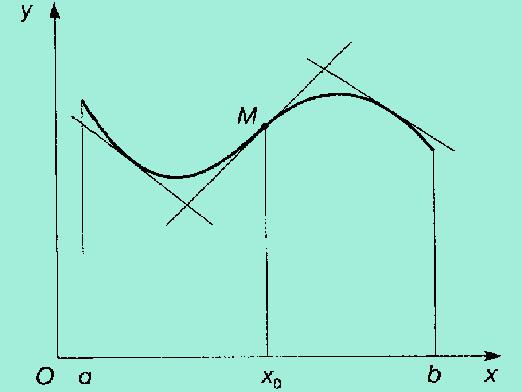
- 함수의 극값 점, 간격 찾기증가 및 감소. 함수의 극값을 찾아 보자. 이를 수행하려면 1 차 미분을 찾아서 0과 같아야합니다.이 시점에서 함수가 증가에서 감소로 바뀔 수 있습니다. 각 간격마다 미분의 부호를 정의합니다. 미분이 양수이면 함수의 그래프는 음수이면 감소합니다.
- 함수의 그래프의 굴곡 지점, 볼록 위 아래로의 간격을 찾습니다.
변곡점이 이제 간단하다는 것을 알 수 있습니다. 2 차 미분을 찾아야 만 0으로 놓을 수 있습니다. 다음으로 각 구간에서 2 차 미분의 부호를 찾습니다. 양수이면 함수의 그래프는 아래로 볼록 해지고 음수이면 위로 향합니다.









