인접한 각도를 찾는 방법?
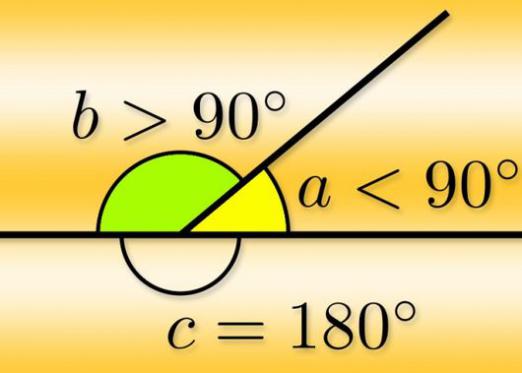
비디오보기

수학은 가장 오래된 정확한 과학입니다.학교, 대학, 연구소 및 대학에서 필수 연구. 그러나 기본적인 지식은 항상 학교에 있습니다. 때로는 수학에서 몇 가지 것을 잊어 버렸기 때문에 자녀가 상당히 어려운 과제를 묻게되고 부모님이 도울 수없는 경우가 있습니다. 예를 들어 기본 각도의 값으로 인접한 각도를 찾는 방법 등이 있습니다. 이 작업은 간단하지만 인접한 객체가 무엇인지를 모르고 그 객체를 찾는 방법을 모르기 때문에 문제를 푸는 데 어려움을 겪을 수 있습니다.
인접한 각도의 정의와 속성 및 문제의 데이터를 계산하는 방법에 대해 자세히 살펴 보겠습니다.
인접 각도의 정의 및 특성
단일 점 형식에서 나오는 두 개의 광선"평면 각도"라는 수치. 이 점을 각도의 꼭지점이라고하고 광선은 그 변입니다. 출발점 너머로 직선을 따라 광선 중 하나를 계속하면 인접이라고하는 다른 각도가 형성됩니다. 이 경우 각 각도마다 두 개의 인접한 각도가 있습니다. 각도의 측면이 동일하기 때문입니다. 즉, 항상 인접한 180도 각도가 있습니다.
인접 각도의 기본 속성은 다음과 같습니다.
- 인접한 각은 공통점과 한면을가집니다.
- 계산이 라디안 단위로 수행되는 경우 인접 각도의 합은 항상 180도 또는 Pi입니다.
- 인접 각도의 사인은 항상 동일합니다.
- 인접한 각의 코사인과 접선은 동일하지만 반대 부호가 있습니다.
이러한 특성으로 인해 인접한 각도를 계산하는 것이 매우 쉽습니다.
인접한 각도를 찾는 법
보통, 인접한 각도의 값을 찾는 문제의 3 가지 변형이 주어집니다
- 기본 각도의 값이 주어집니다.
- 주 각도와 인접 각도의 비율이 주어집니다.
- 수직 각도의 값이 주어집니다.
문제의 각 버전에는 고유 한 솔루션이 있습니다. 그들을 고려하십시오.
기본 각도의 값
작업이 기본 각도의 값을 지정하면인접한 각도를 찾는 것은 매우 간단합니다. 이렇게하려면 기본 각도의 값을 180도에서 뺀 것이면 충분하며 인접한 각도의 값을 얻을 수 있습니다. 이 솔루션은 인접한 각도의 속성을 기반으로합니다. 인접한 각도의 합은 항상 180도입니다.
그러나 기본 각의 값이 라디안 단위로 주어지면문제에서 라디안으로 인접한 각도를 찾는 것이 요구된다면, 180 도의 완전 전개 된 각도의 값이 Pi의 수와 같기 때문에 Pi에서 기본 각도의 값을 빼야 할 필요가있다.
주 각도와 인접 각도의 비율
문제에서는 기본 각도의 값의 각도와 라디안 대신 주 각도와 인접 각도의 비율을 지정할 수 있습니다. 이 경우 솔루션은 비례 방정식처럼 보일 것입니다.
- 우리는 주각의 비율을 변수 "Y"로 나타냅니다.
- 인접한 모서리와 관련된 분수를 변수 "X"로 나타냅니다.
- 각 비율에 해당하는 도수는 "a"와 같습니다.
- 일반 수식은 a * X + a * Y = 180 또는 a * (X + Y) = 180과 같습니다.
- a = 180 / (X + Y) 공식을 사용하여 방정식 "a"의 공통 인자를 찾습니다.
- 그런 다음 공통 인자 "a"의 결과 값에 결정할 각도 분수를 곱합니다.
따라서, 우리는 인접한각도 (도). 그러나 값을 라디안으로 찾으려면 각도를 라디안으로 변환하면됩니다. 이렇게하려면 각도를 각도 Pi에 곱하고 모두 180도로 나눕니다. 결과 값은 라디안 단위입니다.
수직 각도의 값
작업이 기본 각도 값을 제공하지 않고 수직 각도 값을 제공하는 경우 기본 각도 값이 제공되는 첫 번째 단락과 동일한 수식을 사용하여 인접 각도를 계산합니다.
수직 각도는에서 오는 각도입니다.주 요점과 같은 지점이지만 똑같은 반대 방향으로 향하게됩니다. 거울 이미지가 생성됩니다. 이것은 수직 각도가 주 각도와 동일하다는 것을 의미합니다. 교대로, 수직 각도의 인접 각도는 기본 각도의 인접 각도와 동일합니다. 이에 따라 기본 각의 인접 각도를 계산할 수 있습니다. 이렇게하려면 단순히 수직 값을 180도 빼고 주 각도의 인접 각도 값을도 단위로 가져옵니다.
그러나 값이 라디안 단위로 주어지면 총 각도 180 도의 값이 Pi와 같기 때문에 Pi에서 수직 각도 값을 뺄 필요가 있습니다.
또한 유용한 기사를 읽을 수 있습니다. 각도 란 무엇이며 각도는 무엇입니까?