광장의 대각선을 찾는 방법은?

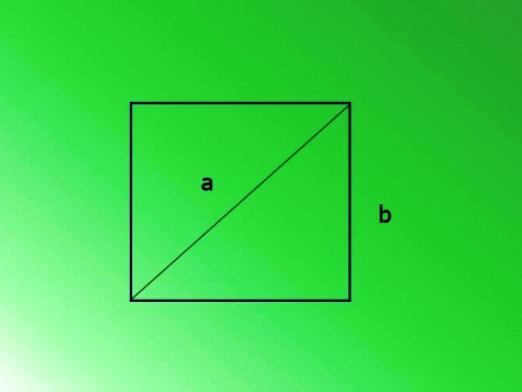
우리가 알다시피, 광장은동등한면을 가진 직사각형, 또는 직각을 갖는 마름모. 정사각형과 같이 직사각형의 대각선은 주어진 그림의 반대 각도를 연결하는 선분입니다. 사각형에서 사각형과 달리 대각선의 크기는 같습니다. 광장의 대각선을 찾는 법을 알아 봅시다.
가장 간단한 방법은 물론 다음과 같습니다.Pythagoras 정리에 따르면 다리의 모든 제곱의 합은 빗변의 제곱과 같습니다. 대각선은 사각형을 두 개의 똑같은 정사각형의 삼각형으로 나누고 그 빗변입니다. 그 다음 측면의 길이를 표시하고 빗변을 찾으십시오. b : b2= a2+ a2, 그것은 다음과 같다. b2= 2a2, b = √ (2a2). = a * √2. 이 방법을 예제로 분석해 보겠습니다.
우리는 정사각형, 한면 - 10cm를 가지며 위의 공식에 따라 대각선은 다음과 같습니다. b = √ (2 * 102). = √ (2 * 100) = 10 * √2 = 14.1cm. 대각선은 빗변이고, 그것은 코사인의 정의에서 찾을 수 있습니다. 인접 다리와 빗변 사이의 각도는 45도, cos 45 = √2 / 2입니다. 또는 우리의 경우 : a / b = √2 / 2 따라서 b = a / (√2 / 2) = a * 2 / √2 = a * √2 * √2 / √2 = a * √2. 기하학의 모든 미묘함을 알고 싶지 않다면 대각선을 찾으려면 단 하나의 관계 만 기억하면됩니다 : 대각선 = 횡 x √2
사각형의 대각선 길이를 찾는 방법은 다음과 같습니다. 위의 식에 따르면 대각선의 길이는 다음과 같습니다. b = 5 * √2 = 5 * 1.4142 = 7.071 cm.
우리는 피타고라스의 정리로 검증합니다 : 5252= 7.0712 25 + 25 = 50이다.
매우 간단합니다. 이 대각선은 정사각형을 둘러싸는 원의 지름이며, 중심 부분은 대각선의 교차점에 있고 측면 길이는 내접 원의 지름과 같습니다.