사각형 영역을 찾는 방법은?

번역에서 "지오메트리"라는 단어는 "토지 측량"을 의미합니다. 그리스어의 "Geos"는 지구이고, "metry"는 측정 값입니다. 우리 시대의 수천 년 전에 고대 이집트인들조차도 나일 강 유역, 유프라테스 강 또는 티그리스 강이 쇄도 한 후에 땅을 재 측정하고 공유해야했습니다. 정확한 수학적 지식 없이는 불가능했습니다. 그래서 실용적인 문제를 해결하기 위해 순전히 적용된 과학 기하학이있었습니다. 토지 구획이 다른 크기와 형태 였기 때문에 다양한 수치의 영역에 대한 정의는 긴급한 과제와 관련이 있습니다. 러시아에서는 1629 년에 "아픈 편지"라는 책이 출판되었으며,이 책에는 다각형의 면적을 측정하는 방법이 설명되어 있습니다. 우리는 오늘이 책에 설명 된 수식을 사용합니다.

직사각형의 영역을 찾는 방법을 이해하려면,"영역"이라는 용어를 정의해야합니다. 각각의 기하학 도형은 수량 중 하나를 특징으로합니다. 평평한 그림의 경우이 영역이 주요 특징입니다. 그림을 한 변의 길이가 1 인 정사각형으로 나누고 총 수를 계산하면 주어진 피겨의 면적을 구합니다. 국제 미터법 SI 시스템의 면적 측정 단위는 평방 미터입니다.

사각형이 호출됩니다.4 개의 직각을 가진 사변형. 통상 로마자 A 및 B에 의해 지정되는 그 측면의 길이에 의해 정의 된 직사각형의 크기. 보통 우리는 그 길이의 사각형의 한쪽면의 크기를 가지고, 다른 - 너비 또는 높이. 그럼 사각형의 면적은 어떻게 구합니까? 우리는 길이와 너비, 즉 변의 크기를 알아야합니다. 우리는 장치의 측면 (1cm, 1mm 1 미터 ...) 정사각형, 직사각형 격자의 표면을 덮이 작은 사각형을 계산할 경우에는 사각형의 한 변을 따라 맞게 큰 사각형의 수의 곱과 동일한 값으로하고, 다른 쪽을 따라 그 번호를 얻는다. 이 양은 필수 영역입니다. 즉, 사각형 영역을 찾는 수식은 다음과 같습니다.

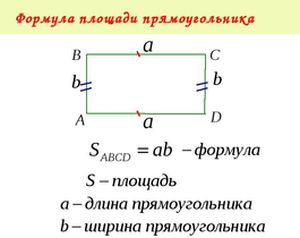
S = (a) * (b)

여기서 a는 사각형의 길이이고, b는 사각형의 너비 (또는 높이)입니다.

그런데, 각 대각선은직사각형을 두 개의 동일한 직사각형 삼각형으로 만들면, 직사각형의 면적은 그러한 삼각형의 면적을 계산하고 그 결과에 2를 곱하여 결정할 수 있습니다. 삼각형 영역의 공식을 알아야하지만 완전히 다른 이야기입니다!